-- AER 213 - Fondamentaux de conception spatiale --

TN n°1

Notions d'Astronomie et d'Astrophysique

- partie 1 -

Repérage et Classification des étoiles

simon.marie@lecnam.net

import numpy as np
import scipy as sc
import matplotlib.pyplot as plt
import time
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
#Option d'affichage et taille de police sur les figures:
fs=20
plt.rc('xtick',labelsize=fs)
plt.rc('ytick',labelsize=fs)
plt.rc('text', usetex=True)
%matplotlib inline

## Constantes utilisées:
c0=299792458     # Vitesse de la lumière dans le vide en m/s
h=6.62607015e-34 # Constante de Planck en J.s
kb=1.380649e-23  # Constante de Boltzmann en J/K

Ce premier TN est destiné à rappeller les notions importantes de bases en astronomie. Ce TN couvre rapidement des notions importantes qui nécessiterait un approfondissement et fond parfois l'objet de cours entier. Cependant l'objectif est uniquement de se familiariser avec ses notions afin d'acquérir des connaissances générales dans ce domaine.

La première chose importante, lorsque que l'on regarde le ciel depuis la terre et que l'on essaye d'observer les mouvements apparents des objets celestes, c'est de se repérer. Comme sur terre, on utilise des coordonnées mais on peut utiliser plusieurs systèmes différents en fonction de la nature de ce que l'on observe.

I - Se repérer dans le ciel: les différents systèmes de coordonnées

Pour repérer un point sur le globe terrestre, on utilise la longitude et la lattitude. Ce système de coordonnée utilise un plan de référence, le plan de l'équateur Pour repérer un astre, une planète ou un satellite sur la sphére céleste, on utilise également des coordonnées. Il existe plusieurs système de coordonnées utilisant différent plan de référence.

1 - Les coordonnées azimutales: Le plan local d'observation

Ce système de coordonnée est très utilisé en astronomie car il permet de situer un objet très rapidement. Les deux coordonnées sont appellés Hauteur et Azimut.

Source Wikipedia

• La hauteur ($h$) fait référence à l'angle entre l'horizon (0°) et le zénith (90°).
• L' Azimut ($A$) correspond à l'angle entre le Nord local et la projection du point considéré sur l'horizon (compté positivement vers l'EST).

Ce système de coordonnée est directement lié à la rotation de la terre sur elle-même et les coordonnées azimutales des astres éloignés vont varier au cours de la journée.

Par exemple le 21 Mars le soleil se lève exactemnt à l'Est et se couche exactement à l'Ouest. Quels sont les coordonnées du soleil à cet instant dans le système azimutale ?

h_lever=...
A_lever=...

Même question pour le soir du 21 Mars:

h_coucher=...
A_coucher=...

2 - Les coordonnées équatoriales: Le plan de l'équateur celeste

Si l'on souhaite définir un système de coordonnée indépendant de l'instant d'observation, il faut s'affranchir de la rotation de la terre. Pour cela on considère que les étoiles sont positionnées sur une sphère fictive supposée fixe: c'est la sphère céleste. Elle correspond à la projection directe de la surface de la terre dans l'espace. On considère alors que les objets lointain (étoiles, galaxies...) sont fixe sur cette sphère. On peut alors leur associer des coordonnées qui seront toujours les mêmes quel que soit le moment d'observation. Ces coordonnées sont l'Ascention droite et la déclinaison:

Source Wikipedia

• L'ascention droite (notée $a$) est la coordonnée longitudinale parcourant l'équateur céleste de 0 à 360°. En pratique l'ascention droite est souvent comptée en heures de 0 à 24h.
• La déclinaison (notée $\delta$) est la coordonnée verticale compté à partir de l'équateur céleste de -90° à +90°.

L'origine de ce système de coordonnée est le premier des deux points d'intersection entre l'ecliptique et l'équateur céleste. Ce point est appellé point vernal. Il est situé dans la constellation des poissons. C'est la position du soleil à midi lors de l'équinoxe de printemps (21 mars).

Ainsi, les coordonnées équatoriales des objets lointain sont relativement constant au cours du temps. En réalité ils varient car l'axe de rotation de la terre oscille periodiquement tous les 26000 ans. Il faut donc préciser l'époque astronomique de référence pour les coordonnées équatoriales. Actuellement l'époque en vigueur est l'époque J2000.

En revanche, concernant le soleil et les objets du système solaire, les coordonnées équatoriales varient d'un jour à l'autre:

Quel sont alors les coordonnées équatoriales du soleil le 21 septembre à midi ?

a=...
dec=...

3 - Les coordonées écliptiques: Le plan de l'écliptique

Un autre système de coordonnée utilisé pour repérer les objets du système solaire est le système de coordonnée écliptique. C'est un système analogue au système équatoriale mais utilisant le plan de l'écliptique à la place de l'équateur céleste. L'origine est également le point vernal mais on parle cette fois de Longitude écliptique (au lieu d'ascention droite) et de latitude écliptique (au lieu de déclinaison).

• La Longitude écliptique $\lambda$ est l'angle entre le point vernal et la projection de l'ojet sur le plan de l'écliptique. Elle varie de $0°$ à $360°$.
• La latitude écliptique $\beta$ est l'angle entre l'objet et sa projection sur l'écplitique. Elle est comptée positivement vers le nord et négativement vers le sud entre 0 et $90°$.

Source Wikipedia

Remarque: Il existe une version héliocentrique de ce système de coordonnée ou l'on place le soleil au centre. Cette version est très utilisé dans les simulations numériques des missions spatiales.

En pratique les deux systèmes de coordonnée équatoriales et écliptiques sont reliés par l'angle $\epsilon$ entre l'écliptique et l'équateur céleste qui correspond à l'inclinaison de l'axe de rotation de la terre. Cette angle $\epsilon$ est appellé *obliquité* et vaut $23.44°$ pour la Terre.

Quels sont les coordonnées écliptiques du soleil lors du solstice d'été ?

lamda=...
beta=...

II - Mesure de distance

En astronomie, les unités de distances sont essentiellement l'unité astronomique (ua), l'année lumière (al) et le Parsecs (pc).

1. L'unité astronomique représente la distance moyenne entre le soleil et la terre soit $1ua=1.496~10^{11}$ m.
2. L'année lumière représente la distance parcourue par la lumière en une année soit $1al=9.4539~10^{15}$ m soit $63197$ ua.
3. le parsec représente la distance à laquelle il faut se placer pour que la distance angulaire d'une unité astronomique représente 1 seconde d'arc soit $1pc=\dfrac{1 ua \times 3600 \times 180}{\pi}=206265$ ua soit $3.085~10^{16}$ m ou $3.26$ al.

ua=1.496e11
al=c0*60*60*24*365.25
pc=180*60*60*ua/np.pi
print(pc/al)
print(pc/ua)

On utilise souvent les unités Mpc (Méga-parsecs) et Gpc (Giga-parsecs) pour les étoiles et les galaxies.

En pratique les mesures de distance d'astres éloignés sont basées sur de nombreuses techniques dont les 3 principales sont:

1. La parallaxe annuelle pour les étoiles situées dans la galaxies ($d<1000pc$). Ces mesures ont été réalisé par le satellite GAIA entre 2013 et 2020.
2. La différence des magnitudes lorsque la luminosité d'un objet de référence est connu (Céphéïdes variables, supernovae de type Ia...)
3. Le décalage vers le rouge (ou redshift) pour les objets du ciel profond très lointain (galaxies, quasars, nébuleuses...).

1. Parallaxe Annuelle

• On mesure l'écart angulaire entre un astre de référence situé plus loin et l'astre dont on souhaite mesurer la distance. On le note $\theta_1$
• On refait la mesure lorsque la terre est de l'autre coté du soleil. On le note $\theta_2$

On peut donc déduire la distance de l'étoile:

$$ d=\dfrac{2 UA}{\theta_1 + \theta_2} $$

que l'on exprime en parsecs:

$$ d=\dfrac{1}{\theta} $$

ou $\theta=(\theta_1+\theta_2)/2$ est la parallaxe annuelle exprimée en seconde d'arc. Ainsi une étoile ayant une paralaxe d'une seconde d'arc est situé à 1 parsec (definition du parsec).

La parallaxe annuelle de Véga (Etoile de la Lyre) a été mesurée à 130.23 millisecondes d'arc, calculer sa distance en parsecs puis en années lumière:

theta=...
d=...
print(d)
print(d*3.26)

2. Luminosité de référence

La magnitude apparente $m$ d'une étoile mesure l'éclat $E$ d'une étoile telle qu'observée sur terre:

$$ m=-2.5\log_{10}(E)+Cste $$

or l'éclat et la luminosité sont relié par $E=L/S=L/(4\pi d^2)$. Les objets observables à l'oeil nu ont une magnitude aparente inférieurs à 6 ($m<6$). Voici quelques examples:

Astre	Magnitude relative
Soleil	-26.7
Pleine Lune	-12.6
Venus (pleine)	-4.6
Mars/Jupiter	-2.9
Sirius	-1.5
Véga	0
Limite visuelle	6
Limite Hubble	31

Attention En pratique la magnitude mesure la luminosité de la partie visible du spectre. On parle de magnitude bolométrique pour se référer à la totalité du spectre ou de magnitude d'une bande spectrale donnée pour se référer à une plage de longueur d'onde donnée (Bande UBVRI pour U-ultraviolet, B-bleu, V-visible, R-rouge, I-infrarouge).

La magnitude absolue $M$ d'une étoile mesure l'éclat $E$ d'une étoile telle qu'observée à une distance fixe $d_{pc}=10$ pc. La relation entre $M$ et $m$ s'écrit donc:

$$ M=m+5-5\log_{10}(d_{pc}) $$

Ainsi on peut déduire la distance $d$ si on connais la luminosité d'une étoile:

$$ d=10 \times 10^{\frac{m-M}{5}} $$

En pratique la mesure des luminosité est possible pour certains astres dont on peut identifier des phénomènes bien connus indépendants de la distance, comme par exemple les variations périodiques de luminosité mis en évidence par Henrietta Leavitt au début du XXème siècle. On peut par exemple identifier des étoiles variables dans les galaxies voisines ou des supernovae encore plus lointaine dont la luminosité est connue.

Dans la galaxie d'Andromède, on a identifié des étoiles variables dont la magnitude apparente vaut $m=19.62$ et la magnitude absolue $M=-4.84$. Calculer la distance de cette galaxie en parsecs puis en années lumière:

d=...
print(d)
print(3.26*d)

3. Redshift

Pour les astres plus éloignés (galaxies, quasars), on peut utiliser la loi de Hubble-Lemaître qui établi un lien entre la distance des galaxie et leur vitesse d'éloignement:

$$ V_r=H_0 d $$

La constante reliant ces deux grandeurs est le paramètre de Hubble $H_0=73.3$ km/s/Mpc. En pratique on mesure la vitesse $V_r$ par l'intermédiaire du décallage vers le rouge $z=\dfrac{\lambda_{obs}-\lambda_{vrai}}{\lambda_{vrai}}$ de certaines raies observé dans le spectre des objets lointains:

$$ V_r=zc $$

Ou $c$ est la vitesse de la lumière en km/s. Cette loi est une approximation des conséquences de la théorie de la relativité générale qui prévoit un univers en expansion et n'est valable que pour les faibles valeurs de $V_r$.

Le quasar 3C 273 situé dans la constellation de la vierge possède un redshift de $z=0.158339$, en déduire sa distance en années lumières:

z=...
d=...
print(d)

III - Classification des étoiles

En astronomie, les étoiles et les objets célestes sont répertoriés dans de nombreux catalogues ayant tous leur particularité. Un catalogue d'étoile recense les données d'un grand nombre d'objets (coordonées, distances, magnitudes, type spectral...).

Les principaux catalogues d'étoiles sont :

1. La désignation de Bayer (1603) (Etoiles par constellation par ordre de magnitude)
2. Le catalogue de **M**essier (1784) (pour les objets du ciel profond visibles avec des instruments amateurs)
3. Le **N**ew **G**eneral **C**atalogue (1888) (pour les nébuleuses et les clusters)

4. Le catalogue **H**enry **D**raper (1924) (Etoiles jusqu'à $m=10$ par ordre d'ascention droite.

5. Le **G**uide **S**tar **C**atalog (1989) (Catalogue des étoiles observées par Hubble)

6. Le Catalogue Gaia (2022) (Catalogue des étoiles recensées par le satellite Gaia)

Chaque catalogue contient de nombreuses informations sur la position, le mouvement propre et le type d'objet recensé. Ces informations sont généralement déduites de la lumière de l'objet observé.

En astrophysique, on utilise la spectroscopie pour étudier la lumière provenant des étoiles. Le principe de la spectroscopie est d'étudier l'intensité de toutes les longueurs d'onde présentent dans cette lumière. On obtient alors le spectre d'une source lumineuse. Les spectromètres reposent la pluspart du temps sur le principe d'une fente de diffraction ou sur un prisme de Newton. Ceux dédiés à l'astrophysique sont montés directement sur des télescopes sur terre (SOPHIE, ESPRESSO) ou dans l'espace (NICMOS, NIRSpec).

Le spectre d'une étoile est composé d'une partie continue caractéristique du rayonnement du corp noir et de parties discrètes caratérisées par des raies d'émission ou d'absorbtion caratériqtiques de la chimie de l'étoile et de son environement.

Loi de Planck sur l'emission du corps noir

La loi de Planck détermine la luminosité $L$ émise à une certaine longueur d'onde $\lambda$ par un corp noir de température $T$:

$$ L(\lambda,T)=\dfrac{2hc^2}{\lambda^5}\dfrac{1}{e^{\frac{hc}{\lambda k_b T}}-1} $$

En dérivant cette relation par rapport à la longueur d'onde on peut trouver la longueur d'onde correspondant à l'emmission maximale, c'est la loi de Wien qui s'écrit sous sa forme simplifiée:

$$ \lambda_{max}=\dfrac{2.898. 10^{-3}}{T} $$

Ainsi n'importe quel élément de matière porté à une température $T$ émet une lumière de spectre continue avec un maximum d'émission à la longueur d'onde $\lambda_{max}$.

Calculer la température minimale du corps noir pour que celui-ci emmette son maximum dans le visible

Tmin=...
print(Tmin)

Calculer la longeur d'onde d'émission maximale d'un corp noir à 310K:

lmax=...
print(lmax/1e-9)

Dans le domaine des longueurs d'ondes visibles (380-720 nm) on peut donc représenter la Luminosité d'un corps noir en fonction de la longueur d'onde (On parle de spectre du corp noir).

def corps_noir(l,T):
    return (2*h*c0**2/l**5)/(np.exp(h*c0/(l*kb*T))-1)

On peut parfois trouver des normalisations utilisant comme référence l'intensité à une longueur d'onde de référence (souvent celle de la raie $H\alpha$ à 656.3nm)

lmda=1e-9*np.arange(150,2500,0.1)

plt.figure(figsize=(16,8))
plt.plot(1e10*lmda,corps_noir(lmda,3000)/corps_noir(656.3e-9,5000),label='$T=3000K$')
plt.plot(1e10*lmda,corps_noir(lmda,4000)/corps_noir(656.3e-9,5000),label='$T=4000K$')
plt.plot(1e10*lmda,corps_noir(lmda,5000)/corps_noir(656.3e-9,5000),label='$T=5000K$')


plt.xlabel('$\lambda$ (\\textup{~\AA})',fontsize=fs)
plt.vlines(x = 3800, ymin = 0, ymax = 1.2, colors='b',linestyles='dashed') 
plt.vlines(x = 7200, ymin = 0, ymax = 1.2, colors='r',linestyles='dashed') 
plt.text(600,1.11,'$Ultraviolet$',fontsize=fs)
plt.text(4500,1.11,'$Visible$',fontsize=fs)
plt.text(8400,1.11,'$Infrarouge$',fontsize=fs)
plt.ylim(0,1.2)
plt.grid(True)
plt.legend(fontsize=fs)

Pour les étoiles, on peut ainsi remonter à leur température de surface en traçant leur spectre et en le comparant à celui d'un corps noir de température donnée.

Spectre d'emission/d'absorbtion

Au sein d'un atome, les électrons ayant un niveau d'énergie donné peuvent absorber l'énergie d'un photon extérieur et changer de niveau d'énergie. Les niveaux d'énergie de chaque atome sont nombreux et possède tous leur propre caratéristiques (orbitale atomique). Pour que le changement de niveau d'énergie puisse se faire, il faut que le photon est exactement l'énergie correspondant à la différence des 2 niveaux d'énergie. L'énergie d'un photon étant inversement proportionel à sa longueur d'onde (E=h\nu=hc/\lambda), un atome ayant des niveaux d'énergie données ne pourra donc absorber que certaines longueurs d'onde. Ces longueurs d'onde spécifiques caractérise le spectre d'absorbtion de l'atome considéré. A l'inverse si l'electron passe à un niveau plus faible, il va émetre un photon de longueur d'onde bien spécifique, on parle de spectre d'émission.

Pour l'atome d'Hydrogène (le plus simple mais le plus abondant dans l'univers) les longueurs d'onde absorbées (resp émises) pour le passage d'un niveau $n$ à un niveau $m$ (resp $m$ à $n$) avec $n<m$, sont données par la formule de Rydberg:

$$ \dfrac{1}{\lambda}=R_H\left(\dfrac{1}{n^2}-\dfrac{1}{m^2} \right) $$

$R_H=10967758.1$ $m^{-1}$ est la constante de Rydberg associée à l'Hydrogène. On parle alors de "série" pour les différentes valeurs de $m$:

• Pour $n=1$, on parle de la série de Lymann (Ultraviolet)
• Pour $n=2$, on parle de la série de Balmer (Visible + ultraviolet)
• Pour $n=3$, on parle de la série de Paschen (Infrarouge)

La série de Balmer est particulièrement utilisée en astrophysique car elle permet de calibrer les instruments dans le visible. On peut représenter la position des raies dans le visible:

def Balmer(m):
    return 3647.05/(1-(4/m**2))

plt.figure(figsize=(16,2))

plt.xlabel('$\lambda$ (\\textup{~\AA})',fontsize=fs)
for m in range(3,8):
    plt.vlines(x = Balmer(m), ymin = 0., ymax = 1.1, colors='k',linestyles='dashed')
    plt.text(Balmer(m)-40,1.1,'m='+str(m),fontsize=12,color='r')

plt.grid(True)
plt.xlim(3800,7200)
plt.ylim(0.5,1.2)
#plt.legend(fontsize=fs)

Ainsi chaque éléments chimique possède ses propres raies ( Spectres du tableau de Mendeleiev) et la spectroscopie permet donc d'étudier les compositions chimiques des milieu traversés par la lumière étudiée.

L'observation du spectre des étoiles (corps noir + raies) permet alors de les classer selon différentes catégories: leur type spectral.

Type Spectral d'une étoile

Le type spectral d'une étoile caractérise sa température de surface et donc la nature de la lumière qu'elle émet. En 1915 Annie Jump Cannon propose de classer les étoiles en 7 types principaux représentés par une lettre du plus chaud au plus froid: O B A F G K M (que l'on retient souvent à l'aide du mnémo "Oh Be A Fine Guy/Girl Kiss Me"). Cette lettre est principalement relié à la température de surface de l'étoile et donc à la longueur d'onde principale de son rayonnement. Chaque type est divisé en 10 sous type numéroté de 0 à 9: ex A0, G2 ou K8.

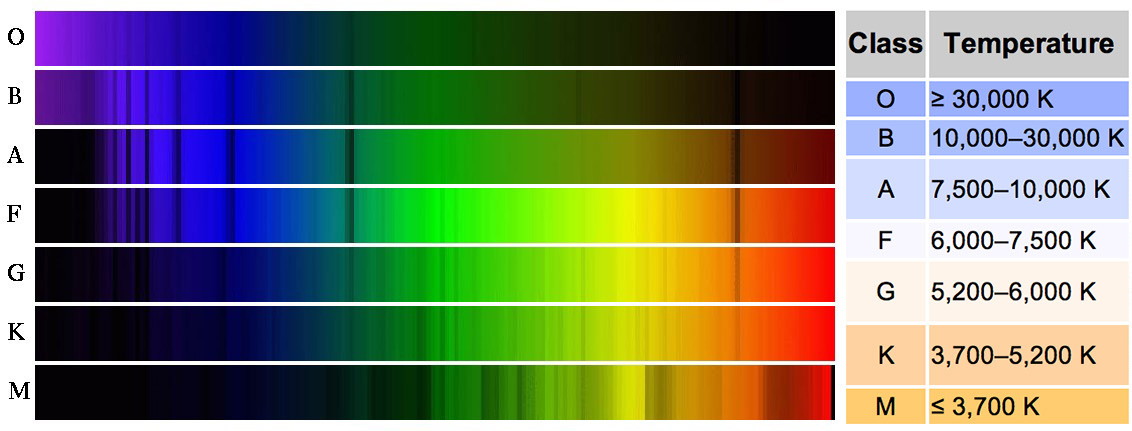
• Les étoiles de type O sont des étoiles bleues, très chaudes ($T>30000 K$). Les raies d'absorbtion de l'Hydrogène (série de Balmer) sont faibles mais visibles. Certaines d’entre elles présentent des raies en émission. -- Ex Meissa ($\lambda Orionis$) --

• Les étoiles de type B sont des étoiles de couleur bleue/blanc et de température de surface de l'ordre de 11 000 à 25 000 K. Leurs spectres sont caractérisés par la présence de raies d'absorption d'hélium neutre (He I) et d'hydrogène neutre (Série de Balmer). -- Ex Bellatrix ($\gamma Orionis$) --

• Les étoiles de type A sont des étoiles de couleur bleuâtre/blanc et de température de surface de l'ordre de 7 600 à 10 000 K. Leurs spectres sont caractérisés par la présence de fortes raies d'absorption d'hydrogène neutre (Série de Balmer), atteignant leur maximum au type A2. Les raies de l'hydrogène sont accompagnées de nombreuses raies métalliques parmi lesquelles la raie K du calcium ionisé (Ca II). -- Ex Vega ($\alpha Lyrae$) --

• Les étoiles de type F sont des étoiles de couleur jaune / blanc et de température de surface de l'ordre de 6 000 à 7 600 K. Leur spectre est dominé par les raies d'absorption du calcium ionisé (Ca II - K et H) qui deviennent plus fortes en intensité que les raies de l'hydrogène neutre (Série de Balmer). Les bandes moléculaires CH (méthylidyne) font leur apparition. -- Ex Caph ($\beta Cassiopeiae$) --

• Les étoiles de type G sont des étoiles de couleur jaune et de température de surface de l'ordre de 4 900 à 6 000 K. Elles présentent des raies d'hydrogène (Série de Balmer) qui s'affaiblissent encore alors que les raies metalliques sont de plus en plus nombreuses et intenses. Les raies du calcium ionisé sont fortes (Ca II H et K) et les bandes moléculaires de CH et de CN deviennent de plus en plus visibles. -- Ex Soleil --

• Les étoiles de type K sont des étoiles de couleur orange et de température de surface de l'ordre de 3 500 à 4 900 K. Les raies d'hydrogène deviennent très faibles alors que les raies metalliques augmentent encore en intensité. En particulier, les raies de calcium ionisé (Ca II) sont très fortes. Les bandes moléculaires de CH sont également très intenses. Les étoiles les moins chaudes de la classe K (à partir de K5) présentent des bandes de TiO (oxyde de titane). -- Ex Arcturus ($\alpha Bootis$) --

• Les étoiles de type M sont des étoiles de couleur rouge et de température de surface de l'ordre de 2 000 à 3 500 K. Leurs spectres sont caractérisés par de fortes bandes moléculaires de TiO (oxyde de titane). -- Ex Betelgeuse ($\alpha Orionis$) --

On trace sur la figure ci-dessous le spectre de 3 types d'étoile. De quel type spectral s'agit-il ?

#! wget https://hpp.education/Lessons/AER213/Files/Spectrum/Star1.dat
#! wget https://hpp.education/Lessons/AER213/Files/Spectrum/Star2.dat
#! wget https://hpp.education/Lessons/AER213/Files/Spectrum/Star3.datq

plt.figure(figsize=(14,7))

Sp1=np.loadtxt('Star1.dat')
plt.plot(Sp1[:,0],Sp1[:,1],label="Etoile 1")

Sp2=np.loadtxt('Star2.dat')
plt.plot(Sp2[:,0],Sp2[:,1],label="Etoile 2")

Sp3=np.loadtxt('Star3.dat')
plt.plot(Sp3[:,0],Sp3[:,1],label="Etoile 3")

T0=3800
plt.plot(lmda*1e10,corps_noir(lmda,T0)/corps_noir(656.3e-9,T0),'--k',label='CN $T='+str(T0)+'K$')

plt.xlim(3800,7200)
plt.xlabel('$\lambda$ (\\textup{~\AA})',fontsize=fs)
plt.ylabel('Intensity (Normaized)',fontsize=fs)
plt.grid(True)
plt.legend(fontsize=fs)

Le diagramme Hersprung-Russel

En pratique on peut observer des étoiles de même type spectral, à des distances similaires mais ayant des luminosités différentes. En effet, si l'on intègre la loi de Planck sur toutes les longueurs d'onde, on retrouve la loi de Stephan-Boltzmann qui donne le flux lumineux total $\phi=\sigma T^4$ ($\sigma$ est la constante de Stephan et s'exprime en fonction des autres constantes: $\sigma=\frac{\pi^2k_b^4}{60c^2\hbar^3}$) et permet de calculer la luminosité d'une étoile $L=S\phi=4\pi R^2 \sigma T^4$. Ainsi, des étoiles de température similaire (même type spectral) mais de luminosité différente, ont nécessairement des tailles différentes. En pratique on regroupe les étoiles dans 7 classes de luminosité différentes par taille décroissante:

• Classe I: SuperGéante (il existe les sous-classes Ia Iab et Ib)
• Classe II: Géantes lumineuses
• Classe III: Géantes
• Classe IV: Sous-géantes
• Classe V: Naines (étoiles de la séquences principales - les plus nombreuses)
• Classe VI: sous-naines
• Classe VII: naines blanches

Le soleil est une étoile de type G2V. C'est donc une naine jaune de la séquence principale.

Le diagramme Hersprung-Russel(HR) est une représentation de la luminosité des étoiles en fonction de leur type spectral.

Il est intéressant de remarquer qu'il n'y a pas de point partout dans ce diagramme et que beaucoup de points se trouve dans la bande centrale appellée "séquence principale" et qui caractérise l'évolution "naturelle" d'une étoile qui parcourt donc au cours de sa vie une trajectoire de droite à gauche dans le diagramme HR.

IV - Mise en pratique: Exploitation d'un catalogue d'étoiles

Afin de mettre en pratique les notions abordées dans ce TN, rien de mieux que l'exploitation des données fournies par un catalogue d'étoile. Le but de cette partie est donc de construire une carte du ciel interactive affichant les grandeurs définies dans le TN.

Le centre de données astronomique de Strasbourg (CDS) héberge une des plus importante base de donnée d'étoiles SIMBAD. Il est consultable en ligne par requêtes html ou bien par l'utilisation d'outils numériques comme Aladin.

On a ici extrait l'ensemble des étoiles visible à l'oeil nu (Magnitude < 6) dans le fichier Simbad_starsV6.txt. Les étoiles visibles étant relativement proches (dans la galaxie) les mesures de distance sont faites par la paralaxe annuelle. Vous pouvez le télécharger sur le serveur avec la cellule suivante (en supprimant le # au début de la ligne):

#! wget https://hpp.education/Lessons/AER213/Files/Simbad_starsV6.csv

Les cellules suivantes proposent l'utilisation de la librairie pandas en python pour exploiter rapidement et simplement les données.

Les colonnes du fichiers sont organisées comme suit:

#|identifier|typ|RA|dec|plx|MagU|MagB|MagV|MagR|MagI|spec.type|ang.size

RA: Ascention droite dec: déclinaison en ° plx: paralaxe en milliseconde d'arc MagV: Magnitude aparente Visuelle

# Chargement du fichier:
VStar=pd.read_csv('Simbad_starsV6.csv',delimiter='|')

# Création des colonnes manquantes
VStar["Size"]=(7-VStar["MagV"]) # Pour afficher les étoiles brillantes en plus gros
VStar["Distance(al)"]=3.2616*(1000/VStar["plx"])

# Calcul de la magnitude Absolue
VStar["Magnitude Abs"]=VStar["MagV"]+5-5*np.log10(VStar["Distance(al)"]/3.2616)


VStar["Color"]=VStar["Magnitude Abs"]

fig=px.scatter(VStar, hover_name="identifier",x="RA", y="dec",
                 color="Magnitude Abs",color_continuous_scale=px.colors.sequential.Hot,size="Size",size_max=8)
fig['layout']['xaxis']['autorange'] = "reversed"
fig.update_layout(
    title="Répartition des étoiles visibles (m<6)",
    xaxis_title="Ascention droite",
    yaxis_title="Déclinaison",
    font=dict(
        family="Maple",
        size=18,
        color="gray"))

fig.add_trace(go.Scatter(x=np.arange(0,360), y=23.44*np.cos(np.pi*(np.arange(0,360)-90)/180),line_color='gray',showlegend=False, name='Ecliptique'))
fig.show()

Les étoiles les plus proches

VStar.sort_values('Distance(al)',)[:10]

Les étoiles les plus brillantes

VStar.sort_values('MagV',)[:10]

Bonus:

A l'aide du catalogue représenter le diagramme HR des étoiles visibles

VStar["BV"]=VStar["MagB"]-VStar["MagV"]

fig=px.scatter(VStar, hover_name="identifier",x="BV", y="Magnitude Abs",
                 color="BV",hover_data=["spec.type","typ","ang.size "],color_continuous_scale=px.colors.sequential.Blackbody,size="Size",size_max=7)
fig['layout']['yaxis']['autorange'] = "reversed"
fig.update_layout(
    title="Diagramme HR des étoiles visibles (m<6)",
    xaxis_title="Composante B-V",
    yaxis_title="Magnitude Absolue",
    font=dict(
        family="Maple",
        size=18,
        color="gray"))
fig.update_xaxes(range=[-1,2])
fig.show()

Références

• [1] F. W. Dyson, Measurement of the Distances of the Stars, Nature 95, 383–387 (1915)
• [2] W.L. Freedman and B.F. Madore, The Hubble Constant, Annu. Rev. Astron. Astrophys. Vol. 48, 2010
• [3] M.Planck, The Theory of Heat Radiation, 1914
• [4] S. Giridhar, Spectral Classification, 2010
• [5] H.N.Russel, Relations Between the Spectra and Other Characteristics of the Stars, Popular Astronomy, 1914

---

from IPython.core.display import HTML
style=open('notebooks.css', "r").read()
HTML(style)

Retour en haut de la page