-- Cours/Projet - AERO-I3 --

Mécanique Spatiale

- La rentrée Atmosphérique -

Trajectoires et paramètres importants

simon.marie@lecnam.net

In [ ]:
import numpy as np
import scipy

import matplotlib
import matplotlib.pyplot as plt

#Option pour afficher les figures dans le notebook et eviter le plt.show():
%matplotlib inline  
plt.rc('xtick',labelsize=14)
plt.rc('ytick',labelsize=14)
In [ ]:
# Constante célestes:
G=6.67408e-11 # Constante de gravitation - 
Rt=6380000 # Rayon terrestre - m
Ms=1.9884e30 # Masse du soleil - kg
Mt=5.9722e24 # Masse de la terre - kg

L'objectif de cette séance est d'étudier la trajectoire de rentrée atmosphérique d'un corps issue d'une orbite initiale connue.

La rentrée atmosphérique peut être annalysée suivant trois phases distinctes:

  1. La manoeuvre de désorbitation visant à quitter l'orbite initiale.
  2. La partie de la trajectoire visant à rejoindre les premières couches de l'atmosphère ($z\sim120$km). (Arc orbitale)
  3. La partie purement atmosphérique souvent dimensionnante pour la mission (Arc atmosphérique). Nous distinguerons l'entrée sans portance dite balistique de l'entrée avec portance dite pilotée.

Lors de cette séance, nous ferons de nombreuses hypothèses simplificatrices pour faciliter les calculs:

  • Orbites coplanaires (2D)
  • Vitesse de rotation des corps céléstes non prise en compte.
  • Coefficients de trainée et de portance indépendant du Mach (Valide en hypersonique mais faux en supersonique).

Ces hypothèses sont celles faites dans la théorie de la rentrée atmosphérique des travaux de Allen et Eggers et permettent néanmoins de conserver les phénomènes importants intervenant dans les trajectoires de rentrée.

Enfin, il ne sera pas question dans cette séance d'étudier en détail les écoulements hypersoniques mis en jeux lors d'une rentrée atmosphérique et faisant intervenir des effets importants de dissociation moléculaire et de ionisation dues aux très fortes températures atteintes. Nous considérerons ici le flux thermique de façon simplifié comme présenté dans la théorie de Allen et Eggers:

$$ \varphi=C_q\sqrt{\rho}u^3 $$

Ou $\varphi$ est en $W.m^{-2}$ et $C_q$ est un paramètre dépendant du type d'atmosphère et du véhicule de rentrée. Pour la terre, on prendra $C_q=1.705~ 10^{-4}$ USI.

On se focalisera dans cette séance sur le calcul des trajectoires possibles en fonction des paramètres de construction des capsules de rentrée (ou atterisseurs). Les trois principales grandeurs que l'on regardera pour dimensionner une mission de rentrée seront:

  • La décélération subit par la capsule (particulièrment pour les rentrées habitées [<10g])
  • Le flux thermique maximal pour le dimensionnement de la protection thermique (masse supplémentaire à prévoir)
  • La pression dynamique maximal pour le dimensionnement des efforts subit par le lanceur pendant la rentrée.
Notes sur l'utilisation du module Orbiter

Afin de pouvoir experimenter les différents scénari de rentrée et de mieux comprendre l'importance de certains paramètres, vous disposez d'un "simulateur" de rentrée en important la classe Capsule du module Orbiter. Dans ce module, les équations du mouvement sont intégrées dans un repère polaire géocentrique.

In [ ]:
# Importation de la classe capsule
from Orbiter import Capsule

Comme toutes les classes en Python, on peut consulter la documentation. En python, la fonction help(Calss) renvoi la documentation de la class ainsi que la documentation de chaque méthode de classe:

In [ ]:
help(Capsule)

I - Désorbitation

La première phase de la rentrée consiste à sortir de l'orbite de "stationnement" pour bifurquer sur une orbite elliptique sécante à la surface d'"atterissage".

Pour cela, on procède à une manoeuvre orbitale en injectant de la quantité de mouvement $\Delta U$ suivant un angle choisit $\omega$.

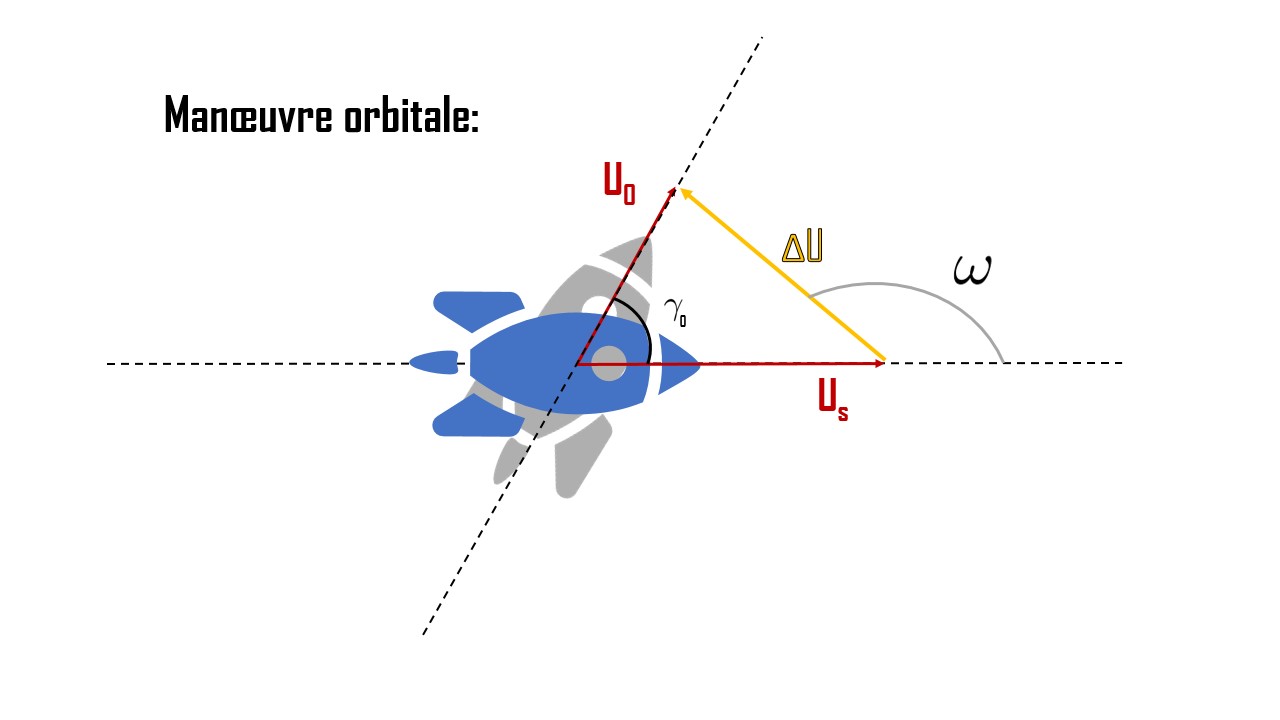
Avec les notations suivantes:

$$ \delta=\dfrac{\Delta U}{U_s} ~~~ \xi=\dfrac{r_0}{r_e} ~~~ k_0=\dfrac{U_0}{U_s} ~~~ k_e=\dfrac{U_e}{U_s} $$

On montre, en utilisant les relations (Al-Kashi) dans le triangle $(U_0,U_s,\Delta U)$ que:

$$ U_0^2=U_s^2+\Delta U^2-2U_s\Delta U \cos(\pi-\omega) $$

soit

$$ k_0=\sqrt{1+\delta^2+2\delta\cos(\omega)}\\ \sin(\gamma_0)=\dfrac{\delta \sin(\omega)}{k_0} $$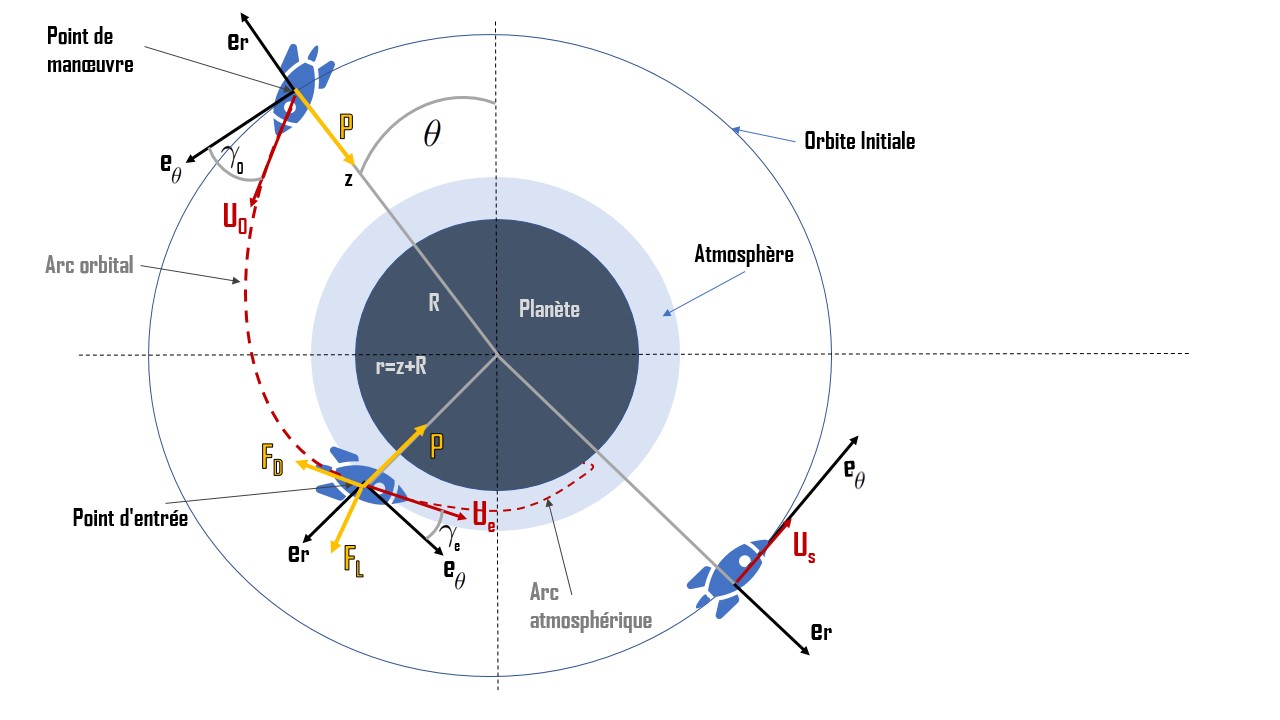

En pratique, on considère une orbite initiale circulaire avec $U_s=\sqrt{\dfrac{GM_t}{r_s}}=\sqrt{\dfrac{GM_t}{r_0}}$.

Ainsi, la conservation de l'énergie sur l'arc orbital donne:

$$ \dfrac{1}{2}U_e^2-\dfrac{GM}{r_e}=\dfrac{1}{2}U_0^2-\dfrac{GM}{r_0} $$

soit:

$$ U_e=U_s\sqrt{2\xi-1+\delta^2+2\delta\cos(\omega)} $$

De la même façon, en utilisant la conservation du moment cinétique $r\dot{\theta}$ sur l'arc orbital soit:

$$ r_e U_e\cos(\gamma_e)=r_0 U_0\cos(\gamma_0) $$

on peut exprimer l'angle de rentrée $\gamma_e$ en fonction des paramètres de manoeuvre $\delta$ et $\omega$ et du paramètre initial $\xi$:

$$ \cos(\gamma_e)=\xi\dfrac{1+\delta\cos(\omega)}{\sqrt{2\xi-1+\delta^2+2\delta\cos(\omega)}} $$

A partir des résultats précédents, créer une fonction permattant de trouver $U_e$ et $\gamma_e$ en fonction de $\Delta U$, $\omega$ et $r_0$

In [ ]:
def rentree(r0,du,w):
    ...
    return ue,ge*180/np.pi

Quel est l'angle et la vitesse de rentrée d'une capsule de rentrée quittant une orbite circulaire de 400km d'altitude avec une manoeuvre du type $(\Delta U, \omega)=(200,180°)$ ?

In [ ]:
rentree(Rt+400000,200,180)

Ainsi, il est possible de déterminer les paramètres d'entrée $(U_e,\gamma_e)$ à partir d'une condition initiale ($U_s$,$r_0$) et des paramètres de manoeuvre ($\Delta U$,$\omega$).

A l'aide du module Orbiter fourni, placer une capsule sur une orbite circulaire à 400km d'altitude

In [ ]:
zs=...
us=...
orb=Capsule(z0=zs,u=us)
print(orb)

Calculer la position de la capsule au bout d'1 heure

In [ ]:
orb.run(...)

Effectuer une manoeuvre de $\Delta u=200$m/s avec $\omega=180°$ puis calculer la nouvelle position de la capsule, 20 minutes après la manoeuvre:

In [ ]:
orb.mvr(...)
orb.run(...)
orb.plotraj()

Comparer les résultats à ceux calculés par la fonction rentree()

Nous allons à présent étudier l'importance des paramètres d'entrée $(U_e,\gamma_e)$ sur la trajectoire et le dimensionnement mécanique de notre capsule de rentrée.

II - Une question de freinage

Considérons tout d'abord le cas le plus simple, en partant d'un corps en chute libre laché d'une altitude de 120km avec une vitesse initiale $U_s$ sous un angle de $90°$ avec l'horizontal local. Ce corp est soumis à son poid $P$ et à une force de trainée $F_d$.

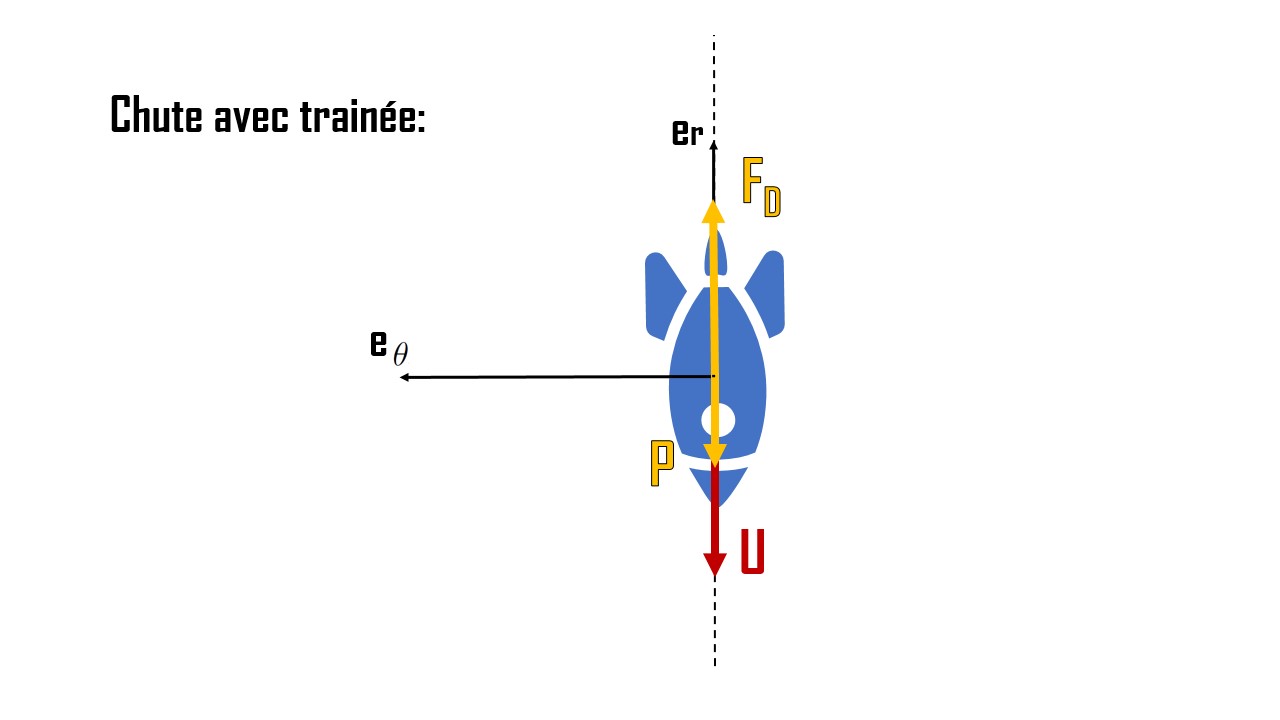
Le bilan s'écrit:

$$ m\dfrac{dv}{dt}=P-F_d=mg_0-\dfrac{1}{2}\rho(z)v(z)^2*S C_d $$

en définissant le coefficient balistique $\beta=\dfrac{S.C_d}{m}$, le bilan devient:

$$ \dfrac{dv}{dt}=\dfrac{mg_0-F_d}{m}=g_0-\dfrac{1}{2}\beta \rho(z)v(z)^2 $$

Ainsi la décélération subi par le corps est directement lié à la force de trainée:

$$ \Gamma=g_0-\dfrac{1}{2}\rho(z)v(z)^2\beta $$

De la même façon que pour l'étape du décollage, on se donnera un modèle d'atmosphère du type:

$$ \rho(z)=\rho_0 e^{-z/z_0} $$

Pour la terre on prendra les valeurs proposées par la théorie de Allen et Eggers $Z_0=6700$m et $\rho_0=1.735$ $kg.m^{-3}$

En utilisant les hypothèses précédentes on peut facilement simplifier les équations du mouvement et montrer que la décélération maximale vaut:

$$ \Gamma_{max}=\dfrac{U_0^2 \sin(\gamma_0)}{2eZ_0} $$

Elle ne dépend donc pas de la forme de la capsule !! En revanche cette décélération maximale est atteinte pour !

$$ Z_g=Z_0\ln\left(\dfrac{\rho_0 Z_0 \beta }{\sin(\gamma_0)}\right) $$

Qui dépend donc de la forme de la capsule à travers $\beta$.

Nous allons essayer de retrouver ce résultat par des simulations.

Le tableau suivant donne quelques exemples de coefficients $\beta$ pour des attérisseurs célèbres:

CapsuleDate$C_d$$S_{ref}$ (m2)$m$ (kg)$\beta$
Gemini1964-19661.52654.15471982$3.2$ $10^{-3}$
Apollo1967-19741.284711.94595806$2.6$ $10^{-3}$
Soyouz1967-today1.32543.69832850$1.7$ $10^{-3}$
Huygens20041.14625.7255318$2.1$ $10^{-2}$
Mars Insight20181.23585.4739358$1.8$ $10^{-2}$
Crew Dragon20201.641810.75217500$2.35$ $10^{-3}$
CST-1002021?1.513719.79238500$3.5$ $10^{-3}$

A l'aide du module Orbiter placer une capsule sur une orbite initiale de 120km d'altitude avec un angle de 90° (à la vertical)

In [ ]:
gem=Capsule(gi=90,z0=120e3)
print(gem)

Par défaut la création de l'instance gem affiche les coordonées de la capsule: $z_0,\theta_0$, son orientation $\gamma$ et sa vitesse initiale $u$.

On peut alors calculer la trajectoire de la capsule en partant de ces conditions initiales. C'est la méthode run() qui permet de faire cela. Cette méthode réalise l'intégration des équations du mouvement.

Lançons la capsule dans l'atmosphère:

In [ ]:
gem.run()

En pratique l'intégration s'arrête lorsque la capsule a atteint le sol (z=0) ou que le nombre d'itérations a atteint une limite fixée (par défaut $10^6$).

Quelle est la vitesse de la capsule lors de l'impact au sol ? Quelle est la durée de la rentrée ?

On peut représenter la trajectoire avec la méthode plotraj():

In [ ]:
gem.plotraj()

Rien de sensationnel en 1D....

Pour charger les données enregistrées pendant la simulation on utilise la méthode load():

In [ ]:
data=gem.load() # On charge les données enregistrtées pendant le "vol"

La méthode nous renvoi la structure du tableau de données "data". Ainsi data[:,0] contient le temps, data[:,1] l'altitude...

Tracer l'évolution de la décélération en fonction de l'altitude et comparer la valeur max à celle estimer plus haut.

In [ ]:
fig=plt.figure(figsize=(10,6),dpi=120)
# On calcul la deceleration maximal et son altitude
Z0,u0=6700,7910
Gm=...
Zg=...
plt.plot(Gm/9.81,Zg/1000,'sr')

# Comparons avec notre simulation:
plt.plot(data[:,7]/9.81,(data[:,1]-Rt)/1000);
plt.ylabel('Alt (km)');plt.xlabel('Deceleration (g)');

Qu'observez-vous ?

Regardons alors l'importance de l'angle $\gamma_e$ dans une trajectoire plus réaliste en 2D.

III - Rentrée balistique (sans portance)

Ici nous considérons que la rentrée se fait sous un angle initial $\gamma_e$. La capsule est soumise aux deux mêmes forces que précédemment mais avec une angle $\gamma$ quelconque:

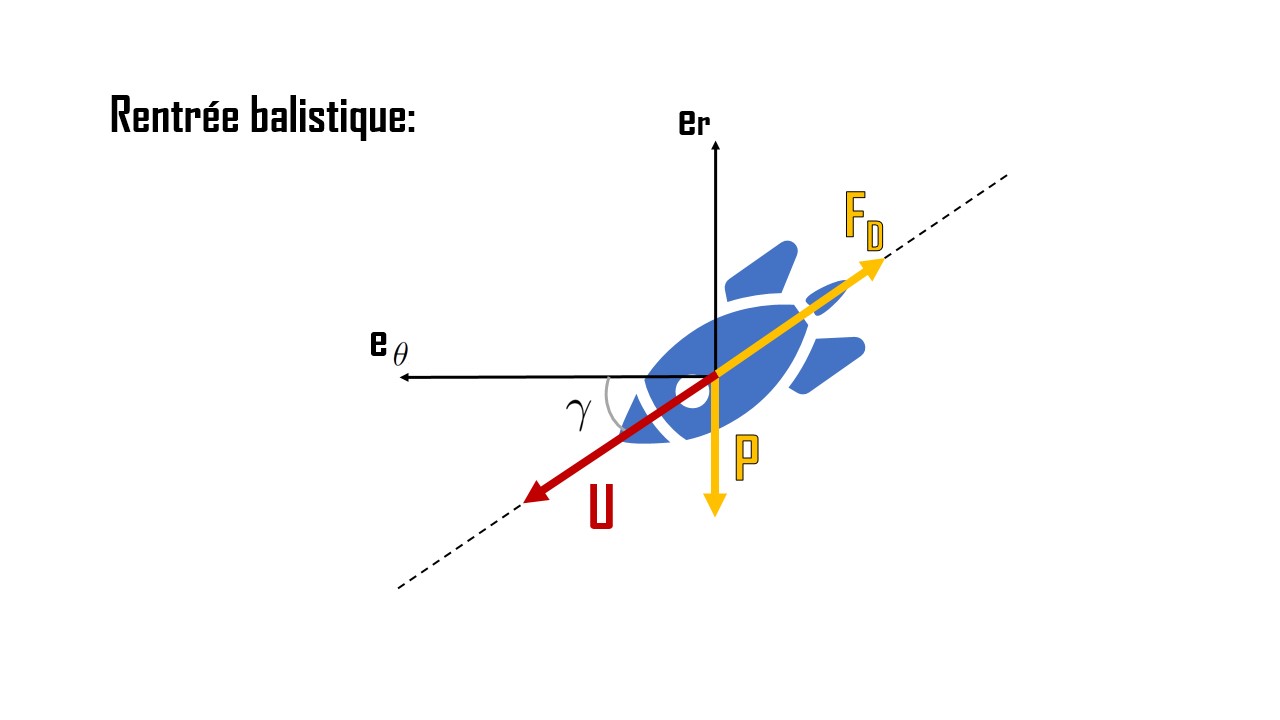
Les équations du mouvement dans le plan polaire $(r,\theta)$ s'écrivent:

$$ m(\ddot{r}-r\dot{\theta}^2) = -P+F_d\sin(\gamma_e)\\ m(r\ddot{\theta}+2\dot{r}\dot{\theta}) = -F_d\cos(\gamma_e) $$

soit en divisant par la masse et en utilisant les notations introduites précédemment:

$$ \ddot{r}-r\dot{\theta}^2 = -\dfrac{\mathcal{G}M_t}{(R_t+r)^2}+\dfrac{1}{2}\rho(r)U^2\beta\sin(\gamma_e)\\ r\ddot{\theta}+2\dot{r}\dot{\theta} = -\dfrac{1}{2}\rho(r)U^2\beta\cos(\gamma_e) $$

Ces équations sont intégrées dans la classe Capsule.

A l'aide du module Orbiter, placer une capsule sur la même orbite que précédemment en changeant uniquement l'angle de rentré à $\gamma_e=6$, puis réaliser le calcul de la trajectoire:

In [ ]:
gem=Capsule(gi=6,z0=120e3)
print(gem)
In [ ]:
gem.run()

Quels est la vitesse de la capsule lors de l'impact au sol ? Quelle est la durée de la rentrée ? Tracer la trajectoire à l'aide de la méthode plotraj()

In [ ]:
fig=plt.figure(figsize=(15,5),dpi=120)
gem.plotraj()

Que remarquez-vous ?

A l'aide de la méthode monit(fig) commenter l'évolution de la décélération et du flux thermique absorbé par la capsule

In [ ]:
fig=plt.figure(figsize=(12,14),dpi=90)
gem.monit(fig)

Conclusion ?

IV - Rentrée pilotée (avec portance)

Les équations du mouvement a intégrer sont sensiblement les mêmes que dans le cas précédent, en ajoutant la force de portance. Le coefficient de portance est supposé constant et proportionel au coefficient de trainée:

$$ finesse=\dfrac{C_L}{C_D} $$

La finesse d'un vehicule de rentrée est plutôt faible ($\sim0.3$) et pouvait atteindre l'unité pour les (feu-)navettes américaines.

En suivant la même procédure que précédemment, étudier la rentrée de la même capsule ayant une finesse de 0.3

In [ ]:
cap=Capsule(...,name='Rentree_port.dat')
print(cap)
In [ ]:
cap.run(dt=0.1)
In [ ]:
fig=plt.figure(figsize=(15,5),dpi=90)
cap.plotraj()
In [ ]:
fig=plt.figure(figsize=(12,14),dpi=90)
cap.monit(fig)
gem.monit(fig)

Comparer alors les deux trajectoires. Que pouvez-vous dire ?

Maintenant, réaliser la même simulation en choisissant un angle de rentrée très faible de l'ordre du demi-degrès

In [ ]:
cap2=Capsule(...,name='Rentree_port2.dat')
cap2.run(dt=0.1)
In [ ]:
fig=plt.figure(figsize=(12,4),dpi=90)
cap2.plotraj()

Qu'observez-vous ?

V - Mission Complète

Maintenant vous devez pouvoir revenir sur terre en un point précis à partir d'une orbite donnée:

En partant d'une capsule de type "Orion" de finesse $0.26$, initialement sur une orbite circulaire de 350 km d'altitude, vous devez atterir au point $\theta = 272°$ avec les contraintes suivantes: $\Gamma<10g$ et $\varphi<1000 kW/m^2$, précision$<100m$

In [ ]:
cap3=Capsule(...)
cap3.run(...)
cap3.mvr(...)
cap3.run(...)
cap3.plotraj()
print("precision= "+str(Rt*(((180*cap3.theta/np.pi)-272)*np.pi/180))+" m")

Y'a t'il unicité de la solution ? Si non comment pourrait-on calculer la manoeuvre optimale nécéssitant le moins de carburant ?

VI - Quelques notions sur les dispositifs de freinages

Comme nous l'avons vu, le flux thermique auquel est soumis le véhicule de rentrée peut rester important même avec des angles de rentrée relativement faibles ($500-800$ $kW/m^2$). Ainsi la protection thermique devient indispensable pour assurer l'intégrité du véhicule.

Deux solutions sont possibles:

  • les protections rayonnantes pour les rentrées plannées à faibles $\gamma_e$
  • les protections ablatives pour les rentrées balistiques à $\gamma_e$ plus élevé engeandrant des flux thermique plus importants.

1 - Protections thermiques Rayonnantes

Pour ce type de protection, la paroi externe du bouclier emet un flux thermique par rayonement qui est en équilibre thermique avec le flux convectif incident. D'après la loi de Stephan-Boltzmann, on a donc en notant $T_p$ la température de paroi:

$$ \varphi_{i}=\varphi_{rayonement}=\epsilon\sigma T_p^4 $$

soit:

$$ T_p=\left(\dfrac{\varphi_i}{\epsilon\sigma}\right)^{(1/4)} $$

$\sigma=5.670367~ 10^{-8}$ $W.m^{-2}.K^{-4}$ $\epsilon$: émissivité du materiaux

Voici quelques candidats pour la construction de ce type de protection

Materiaux$T_{max}$ °C$\epsilon$
Fibre de silice13000.88
niobium13000.89
Fibre de zircone14000.84
Tantale15000.64

En se basant sur vos résultat, estimer les températures de paroi des différentes rentrées que vous avez effectuées

In [ ]:
In [ ]:

2 - Protections thermiques Ablatives

Ce deuxième type de protection est basée sur le principe de l'absorbtion de la chaleur par des réactions endothermiques de type changement d'état (fusion, sublimation, vaporisation...).

Dans ce cas, la surface subissant le flux thermique reste à température constante $T_a$ appellée température d'ablation. On peut écrire un modèle très simplifié d'évolution du front d'ablation $s$:

$$ \varphi(t)\sim\rho_a H_a \dfrac{\partial s}{\partial t} $$
Materiaux$T_{a}$ (°C)$\rho$ (kg/$m^3$)$H_a$ (kJ/kg)
ULD100 MDac107325045000

A partir des résultats de la dernière simulation, estimer la taille et la masse du bouclier thermique a utiliser pour absorber le flux thermique incident

In [ ]:
T=cap.load()
...

Conculsion

3 - Parachute supersonique

Lorsque le nombre de Mach local a atteint des niveaux supersoniques raisonable ($\sim 1.5$), on peut utiliser un système de freinage basé sur le déploiement d'un parachute supersonique. En pratique la décélération de basse atmosphère dépend énormément de la mission et du type d'atmosphère. Sur ce sujet, on pourra consulter les références données en conclusion.

In [ ]:
from IPython.display import YouTubeVideo
YouTubeVideo('AcAgnQ9K7UY',width=600,height=400)

Conclusion

Rédigez une synthèse de toutes les notions que vous avez parcourues dans ce projet.

Références

Voici quelques références qui ont servi a mettre au point ce notebook. Les lecteurs intéressés pourront approfondir de nombreux sujets en les parcourant.

In [1]:
from IPython.core.display import HTML
style=open('notebooks.css', "r").read()
HTML(style)
Out[1]:

Retour en haut de la page